Cálculo I: Números Reais

Neste post falaremos dos Números Reais e suas propriedades na introdução ao Cálculo.

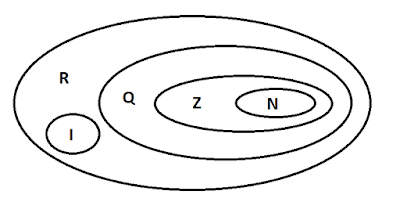
O conjunto dos números reais (ℝ) é formado pela união dos conjuntos Naturais (ℕ), Inteiros (ℤ), Racionais (ℚ) e Irracionais (𝕀).

No conjunto dos números Naturais (ℕ) existe uma propriedade importante, denominada Princípio da Indução Finita (para mais detalhes, clique aqui). Essa propriedade é muito utilizada no estudo de sequências.

Com as propriedades existentes no conjunto dos ℝ, assim como no conjunto dos ℕ, ℤ e ℚ, é possível que se defina as operações de ADIÇÃO e MULTIPLICAÇÃO. Neste ponto definimos o que é um Corpo.

Definição 1: Um corpo é um conjunto M diferente de vazio que possui duas operações: ADIÇÃO ⊕ e MULTIPLICAÇÃO ⊗ de modo que satisfaça as seguintes propriedades:

a) Associativa: Dados a,b,c ∈ M são verdadeiras as seguintes relações:

(a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)

(a ⊗ b) ⊗ c = a ⊗ (b ⊗ c)

b) Comutativa: Dados a,b ∈ M, são verdadeiras as seguintes relações:

a ⊕ b = b ⊕ a

a ⊗ b = b ⊗ a

c) Elemento neutro da adição: Deve existir 0 ∈ M tal que a ⊕ 0 = a, para todo a ∈ M.

d) Elemento neutro da multiplicação: Deve existir 1 ∈ M, tal que a ⊗ 1 = a, para todo a ∈ M.

e) Elemento simétrico ou oposto da adição: Deve existir -a ∈ M para cada elemento a ∈ M tal que:

a ⊕ (-a) = 0 (elemento neutro da adição).

f) Elemento inverso da multiplicação: Deve existir a⁻¹ ∈ M* para cada a ∈ M de forma que:

a ⊗ (a⁻¹) = 1 (elemento neutro da multiplicação)

g) Propriedade distributiva da multiplicação de uma adição: Para quaisquer elementos a, b, c ∈ M, deve ser válida a seguinte igualdade:

a ⊗ (b ⊕ c) = a ⊗ b ⊕ a ⊗c

De posse dessa definição temos que, dos conjuntos acima mencionados, apenas os conjuntos ℝ e ℚ satisfazem a definição acima para as operações de adição e multiplicação usuais e, portanto, podem ser chamados de Corpo.

---

Exercícios resolvidos:

Exercício 1: Mostre que o conjunto dos números Racionais (ℚ) forma um corpo segundo as operações de adição e multiplicação usuais:

O conjunto ℚ é formado por números que podem ser escritos por:

Onde tanto a quanto b são números Inteiros (ℤ), onde b ≠ 0.
Sejam os três números Racionais a seguir:

Vamos verificar as propriedades:

Propriedade a) Associativa:
Esta propriedade é válida para a soma e a multiplicação usuais já que, para quaisquer a,b,c,d,e,f ∈ ℤ são verdadeiras as igualdades:

Propriedade b) Comutativa:
Esta propriedade é válida para a soma e a multiplicação usuais já que, para quaisquer a,b,c,d ∈ ℤ são verdadeiras as igualdades:

Propriedade c) Elemento neutro da adição:
É válida pois o 0 pertence ao conjunto dos números Racionais.


Propriedade d) Elemento neutro da multiplicação:
É válida pois o 1 pertence ao conjunto dos números Racionais.

Propriedade e) Elemento simétrico ou oposto da adição:
É válida pois para qualquer elemento que pertença aos Racionais, o seu simétrico também pertence.

Propriedade f) Elemento inverso da multiplicação:
É válida pois para qualquer elemento que pertença aos Racionais, o seu inverso também pertence.

Propriedade g) Propriedade distributiva da multiplicação de uma adição:
É válida pois para qualquer elemento que pertença aos Racionais, a igualdade abaixo é verdadeira:

Por satisfazer todas as propriedades, temos que os números Racionais formam um corpo.

Exercício 2: Por que o conjunto dos números Naturais (ℕ) não é um corpo?
Por não possuir números negativos contata-se que a propriedade e) não pode ser cumprida. Além dela, a Propriedade f) também não.

Exercício 3: Por que o conjunto dos números Irracionais (𝕀) não é um corpo?

Por não possuir os números 0 e 1, não satisfaz as Propriedades c) e d).
Surge, destas propriedades, a seguinte Proposição:

Proposição 1: Para todo conjunto que seja um corpo, é verdadeiro:
1 - O elemento neutro é único;
2 - A unidade é única;
3 - Para cada elemento x do conjunto, existe um único elemento simétrico;
4 - Para cada elemento x do conjunto, existe um único elemento inverso multiplicativo;
5 - Se a,b,c pertencem ao conjunto de tal forma que a+b = a+c então, b = c;
6 - Dados a,b que pertençam ao conjunto, é verdadeiro:
-(-a) = a
-(a+b) = (-a) + (-b)
(-a)*b = a*(-b)
(-a)*(-b) = a*b
7 - Dados a,b que pertençam ao conjunto, é verdadeiro dizer que:
a*b = 0 se, e somente se, a = 0 ou b = 0
8 - Dados a,b que pertençam ao conjunto e sejam diferentes de zero, é verdadeiro dizer que:
(a⁻¹)⁻¹ = a
(a*b)⁻¹ = a⁻¹ * b⁻¹

Definição 2: Um corpo ordenado é um corpo K que possua um subconjunto P não vazio denominada conjunto dos números positivos de K, tal que:
a) Para todo a,b ∈ P tem-se que a+b e a*b ∈ P.
b) Para cada a ∈ K uma e somente uma das afirmativas abaixo é verdadeira:
ou a = 0, ou a ∈ P ou -a ∈ P

Definição 3: Seja C um corpo ordenado e seja S um subconjunto não vazio de C, define-se que:
a) S é limitado superiormente em C caso exista algum termo a ∈ C que seja maior ou igual a todos os termos de S. Dizemos nesse caso que a é uma cota superior de S em C. Se a for a menor cota superior de S em C, chamamos a de supremo de S em C.
b) S é limitado inferiormente em C caso exista algum termo b ∈ C que seja menor ou igual a todos os termos de S. Dizemos nesse caso que b é uma cota inferior de S em C. Se b for a menor cota inferior de S em C, chamamos b de ínfimo de S em C.
c) S é limitado em C quando possui cota inferior e superior em C.

---

Exercício resolvido:
Exercício 4: Mostre que o conjunto A = [3, 10) é limitado em ℝ.
De fato, basta tomarmos 2 ∈ ℝ e 15 ∈ ℝ, onde 2 é uma cota inferior e 15 é uma cota superior. No caso temos 3 como ínfimo de A em ℝ e 10 como supremo de A em ℝ.

---

Em outras palavras, o supremo de um conjunto é um valor tal que seja maior ou igual a todos os valores do conjunto porém não existe valor "intermediário" entre ele e o maior valor do conjunto. Esta afirmação só é verdadeira quando o supremo é o próprio maior valor do conjunto.
O raciocínio análogo ocorre para o ínfimo, devendo ser ele o menor valor do conjunto.

Definição 4: Um corpo ordenado completo é um conjunto tal que todo subconjunto dele, limitado inferiormente, admite ínfimo nele.

---

Exercício resolvido:
Exercício 5: Mostre que ℚ não é um corpo ordenado completo.
Dado o conjunto A = {x ∈ ℚ / x² > 2} temos que o ínfimo do conjunto √2 ∉ Q. Desta forma, este subconjunto de ℚ não possui ínfimo em ℚ, mas apenas em ℝ. (Veja também: Mostre que √2 não é Racional).

---

O conjunto dos ℝ é um corpo ordenado completo.

PS: O conjunto dos números Naturais pode ser definido com o 0 (zero) ou sem ele. Esta definição fica a critério do professor.

Exercício Resolvido - Conjuntos

Em uma sala de aula, 21 alunos falam francês, 20 não falam inglês, 32 só falam inglês e 45 só falam um desses dois idiomas. Pergunta-se:
a) Qual o total de alunos da sala?
b) Quantos falam os dois idiomas?

Solução:
Então temos os seguintes casos:
Alunos que falam somente francês: Vou chamar de F
Alunos que falam somente inglês: Vou chamar de I
Alunos que falam os dois idiomas: Vou chamar de IF
Alunos que não falam nenhum idioma: Vou chamar de N

F + IF = 21, pois 21 falam francês
F + N = 20, pois 20 não falam ingês
I = 32, pois 32 falam somente inglês
F + I = 45, pois 45 falam um, e apenas um, desses dois idiomas.

Assim:
F + I = 45
I = 32
Temos que F = 13

F = 13
F + IF = 21
IF = 8

F = 13
F + N = 20
N = 7

Assim, o total de aluno é:
F + I + IF + N = 13 + 32 + 8 + 7 = 60 alunos

IF = 8, logo 8 falam os dois idiomas.

Exercício resolvido - Conjuntos

Em um banco, qualquer funcionário da carreira de Auditor é formado em pelo menos um dos cursos: Administração, Ciências Contábeis e Economia.
Um levantamento forneceu as informações de que:

I. 50% dos Auditores são formados em Administração, 60% são formados em Ciências Contábeis e 48% são formados em Economia.

II. 20% dos Auditores são formados em Administração e Ciências Contábeis.

III. 10% dos Auditores são formados em Administração e Economia.

IV. 30% dos Auditores são formados em Ciências Contábeis e Economia.

Escolhendo aleatoriamente um Auditor deste banco, a probabilidade de ele ser formado em pelo menos dois daqueles cursos citados é:

Solução:
Inicialmente, sabemos que um auditor é formado em pelo menos um dos cursos:
Administração
Ciências contábeis
Economia

Então podemos ter:
Formados em Administração apenas: vou chamar esse grupo de A
Formados em Ciências Contábeis apenas: vou chamar esse grupo de CC
Formados em Economia apenas: vou chamar esse grupo de E
Formados em Administração e Ciências Contábeis apenas: vou chamar esse grupo de ACC
Formados em Administração e Economia: vou chamar esse grupo de AE
Formados em Economia e Ciências Contábeis: vou chamar esse grupo de ECC
Formados nos três cursos: vou chamar esse grupo de AECC

Assim, sabemos que:
Total:
(1) A + CC + E + ACC + AE + ECC + AECC = 100%
Formados em administração:
(2) A + ACC + AE + AECC = 50%
Formados em Ciências Contábeis:
(3) CC + ACC + ECC + AECC = 60%
Formados em Economia:
(4) E + AE + ECC + AECC = 48%
Formados em Administração e Ciências Contábeis:
(5) ACC + AECC = 20%
Formados em Administração e Economia:
(6) AE + AECC = 10%
Formados em Ciências Contábeis e Economia:
(7) ECC + AECC = 30%

Queremos saber a porcentagem de formados em pelo menos dois cursos, ou seja:
AE + ACC + ECC + AECC = ???

Das equações (2), (3) e (4), podemos obter valores para A, CC e E:
A = 50 - ACC - AE - AECC
CC = 60 - ACC - ECC - AECC
E = 48 - AE - ECC - AECC

Substituindo esses valores em (1):
(50 - ACC - AE - AECC) + (60 - ACC - ECC - AECC) + (48 - AE - ECC - AECC) + ACC + AE + ECC + AECC = 100
158 - 3AECC - 2ACC - 2AE - 2ECC + ACC + AE + ECC + AECC = 100
58 - 2AECC - ACC - AE - ECC = 0
ACC + AE + ECC + 2AECC = 58

Somando-se as equações (5), (6) e (7) temos:
ACC + AE + ECC + 3AECC = 60

Combinando essas duas equações sublinhadas, percebemos que AECC = 2%
Logo ACC + AE + ECC + AECC = 56%

Assim, escolhendo aleatoriamente um Auditor deste banco, a probabilidade de ele ser formado em pelo menos dois daqueles cursos citados é de 56%.

Exercício Resolvido - Conjuntos

Em uma pesquisa realizada num grupo de 100 alunos, constatou-se que 42 falam inglês, 12 falam inglês e francês, 18 falam espanhol e inglês e 16 falam espanhol e francês. O numero de alunos que falam espanhol é precisamente 50% maior que i número daqueles que falam francês. Com base nessas informações, julgue os itens abaixo como verdadeiros ou falsos.

( ) O numero de alunos que falam frances é igual a 0,6 do numero dos que falam espanhol.

( ) Se 9 dos alunos consultados falam 3 linguas e 5 não falam nenhuma delas, então mais da metade dos alunos falam francês.

( ) Se 9 dos alunos consultados falam as três linguas e 5 não falam nenhuma delas, então exatamente 24 desses alunos não falam apenas inglês.

Solução:
Total: 100 alunos
Línguas: Inglês, francês e espanhol.
Podemos ter alunos que:
Não falam nada: N
Falam só inglês: In
Falam só francês: F
Falam só espanhol: E
Inglês e francês: InF
Inglês e espanhol: InE
Espanhol e francês: EF
Inglês, espanhol e francês: InEF

Sabemos que:
In + F + E + InF + InE + EF + InFE + N = 100          (1)
42 = In + InE + InF + InEF                                         (2)
12 = InF + InEF                                                          (3)
18 = InE + InEF                                                          (4)
16 = EF + InEF                                                           (5)
E + EF + InE + InEF = 1,5*(F + EF + InF + InEF)  (50% maior). 

Trabalhando essa igualdade:

E + InE = 1,5F + 0,5EF + 1,5InF + 0,5InEF               (6)

Assim, usando (2) em (1):
42 + F + E + EF + N = 100
F + E + EF + N = 58                                                  (7)

Primeira afirmação:
Falsa, pois o número de alunos que falam espanhol é precisamente 50% maior que o número daqueles que falam francês.
Assim, vou chamar de EE os alunos que falam espanhol (E + InE + EF + InEF) e de FF (F + EF + InF + InFE) os que falam francês.
Do exercício temos que:
EE = 1,5FF, logo
FF = 0,666666EE, e não 0,6 apenas.

Segunda afirmação:
InFE = 9 e N = 5, então FF > 50.
De (3), InF = 3
De (4), InE = 9
De (5), EF = 7
De (2), In = 21

Combinando todos esses dados em (1):
21 + F + E + 3 + 9 + 7 + 9 + 5 = 100
F+E = 46

Usando (6):
E + 9 = 1,5F + 0,5*7 + 1,5*3 + 0,5*9
E - 1,5F = 3,5

Tendo o sistema:
E + F = 46
E - 1,5F = 3,5
2,5F = 42,5
F = 17

Assim, FF = F + InF + EF + InFE = 17 + 3 + 7 + 9 = 36 < 50, falsa.

Terceira afirmação:
Falsa também. Já que o número de alunos que falam apenas inglês é 21, sendo, portanto, o número dos que NÃO falam apenas inglês 100-21 = 79

Exercício Resolvido - Número de elementos de conjuntos

Se X é um conjunto com um número finito de elementos, n(X) representa o número de elementos do conjunto X. Considere A,B e C com as seguintes propriedades:

n(A U B U C) = 25
n(A - C) = 13
n(B - A) = 10
n(A ∩ C) = n[C - (A U B)]
Qual o maior valor possível de n(C) ?

Solução:

Da primeira informação do exercício temos que C pode ter 25 elementos

De n(A - C) = 13, temos que A possui 13 elementos que C não possui. Combinada com a informação anterior, podemos concluir que C pode ter então, no máximo 12 elementos.

Neste ponto, vamos então supor que n(C) = 12. Se for menos, haverá alguma contradição com as informações do exercício.

Relações:

n(X ∩ Y) = n(X) + n(Y) - n(X U Y)

n(X - Y) = n(X) - n(X ∩ Y)

Assim:

Adotando que (A U B) = K, para simplificar, de n(A U B U C) = 25 temos:

n(K U C) = n(K) + n(C) - n(K ∩ C)

n(K U C) = n(K) + 12 - n(K ∩ C) = 25

n(K) - n(K ∩ C) = 13

Mas:

Equação 1) n(K) - n(C ∩ K) = n(K - C) = 13

De n(A - C) = 13 temos:

n(A) - n(A ∩ C) = 13

Equação 2) n(A)  = n(A ∩ C) + 13

De n(A ∩ C) = n[C - (A U B)] temos:

n(A ∩ C) = n(C - K)

Usando a equação 2)

Equação 3) n(A) - 13 = n(C - K)

Mas:

n(C - K) = n(C) - n(C ∩ K)

Usando a equação 1)

n(C - K) = n(C) + 13 - n(K)

Assim:

n(A) - 13 = n(C) + 13 - n(K) = 12 + 13 - n(K) = 25 - n(K)

Equação 4) n(A) = 38 - n(K)

De n(B - A) = 10 temos:

n(B - A) = n(B) - n(B ∩ A) = n(B) - [n(B) + n(A) - n(B U A)] = 10

n(B - A) = n(B) - n(B) - n(A) + n(K) = 10

n(B - A) = - n(A) + n(K)

Usando equação 4)

n(B - A) = -38 + n(K) + n(K) = 10

2*n(K) = 48

n(K) = 24

n(A) = 14

n(C - K) = n(A ∩ C) = 1

n(C ∩ K) = 11

Temos que:

n(K ∩ C) = n[(A U B) ∩ C] = n[(A ∩ C) U (B ∩ C)] = n(A ∩ C) + n(B ∩ C) - (A ∩ B ∩ C) = 11

Equação 5) n(A ∩ C) + n(B ∩ C) - (A ∩ B ∩ C) = 11

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + (A ∩ B ∩ C)

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - [n(A ∩ C) + n(B ∩ C) - (A ∩ B ∩ C)]

Usando a equação 5) temos

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - 11

Substituindo valores

25 = 14 + n(B) + 12 - 1 - 11

n(B) = 11

Ou seja, temos resultados viáveis considerando que n(C) = 12. Como este é o maior valor possível segundo as duas primeiras hipóteses, então n(C) não pode ser mais que 12. Logo, o máximo de elementos que C pode ter é 12.

Uma solução numérica seria:
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14};
B = {14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24};
C = {14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25}.

Exercício Resolvido - Conjuntos

Em um hotel há 100 pessoas, 30 comem porco, 60 comem galinhas e 80 comem alface. Qual é o maior número de pessoas que não comem nem porco nem galinha?

Solução:

Sei que 70 não comem porco, 40 não comem galinhas e 20 não comem alface.

Das 70 que não comem porco, podemos ter que 40 delas, não comam galinha também. Desta forma, 40 não comem nem galinha nem porco. Dessas 40, 20 podem não comer alface. Assim:

O número máximo das pessoas que não comem carne é 40, e que não comem nenhuma das comidas, 20.

Assim fica:

20 não comem NADA
30 comem os 3
30 comem galinha e alface
20 comem só alface.

Exercício Resolvido - Número de elementos de um conjunto

Dados os conjuntos A, B e C tais que:

n(B U C) = 20; 

n(A ∩ B)= 5; 

n(A ∩ C)= 4; 

n(A ∩ B ∩ C) = 1; 

n(A U B U C) = 22. 

Nessas condições, o número de elementos de A - ( B ∩ C) é igual a:

a)10
b)9
c)8
d)7
e)6

Solução:

Dados:
n(B U C) = 20
n(A ∩ B)= 5 -> A e B tem 5 elementos em comum.
n(A ∩ C)= 4 -> A e C tem 4 elementos em comum.
n(A ∩ B ∩ C) = 1 -> Existe 1 elemento que é comum aos três conjuntos
n(A U B U C) = 22

n(B U C) = n(B) + n(C) - n(B ∩ C)
n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

Da segunda equação temos:
22 = n(A) + n(B) + n(C) - 5 - 4 - n(B ∩ C) + 1 = n(A) + n(B) + n(C) - 8 - n(B ∩ C)
30 = n(A) + n(B) + n(C) - n(B ∩ C)

Da primeira equação temos:
20 = n(B) + n(C) - n(B ∩ C)

Fazendo a subtração delas:
30 = n(A) + n(B) + n(C) - n(B ∩ C)
20 = n(B) + n(C) - n(B ∩ C)
10 = n(A)

Das afirmações do exercícios, sabemos que existe apenas 1 elemento que pertence a todos os conjuntos.
Desta forma, B ∩ C tem apenas 1 elemento que pertence ao conjunto A. 

Assim:

A - ( B ∩ C) = 10 - 1 = 9

Letra b)