Exercício resolvido - Associação mista de resistores
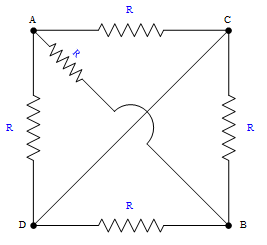
Calcule a resistência equivalente da associação mista de resistores entre os pontos A e B no circuito abaixo:
Solução:
Neste exercício, tem-se dois curtos formando um "X" no meio do quadrado. Como já comentado nos outros casos, a melhor forma de visualizar a disposição dos resistores é unindo os pontos ligados por curto. Neste caso, o vértices do quadrado podem ser transformados em um ponto só.Assim, os pontos A e D podem ser considerados como um mesmo ponto. Da mesma forma, os pontos B e C. Unindo, primeiramente, os pontos A e D temos:
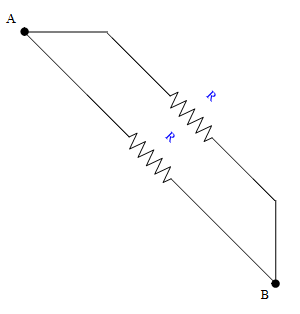
Unindo agora os pontos B e C:
Assim, fica fácil perceber que todas as resistências estão em paralelo. Como todas elas são iguais, tem-se que a resistência equivalente entra os pontos A e B é R/4.
Para saber mais sobre associação de resistores, veja 5 Exercícios Resolvidos de Associação de Resistores Para Você Fixar o Assunto