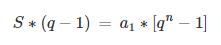Dedução das fórmulas de uma PG e explicação
Dando continuidade às aulas, nada mais coerente do que, após uma aula de PA, a aula de PG.
Assim como a PA, a PG é uma sequência definida por um termo inicial, geralmente chamado de a₁ e uma razão, geralmente chamada de q.
Diferentemente da PA, na PG os termos da sequência são obtidos pelo produto do termo anterior pela razão, ou seja:
a₂ = a₁*q
a₃ = a₂*q = (a₁*q)*q = a₁*q²
a₄ = a₃*q = (a₁*q²)*q = a₁*q³
...
an = a(n-1)*q = a₁*q⁽ⁿ⁻¹⁾
Uma propriedade importante de observarmos é que o produto dos termos equidistantes ao termo central de um PG é sempre igual. Sendo mais claro:
Produto do primeiro termo com o último termo:
a₁*an = a₁*(a₁*q⁽ⁿ⁻¹⁾) = a₁²*q⁽ⁿ⁻¹⁾
Produto do segundo termo com o penúltimo termo
a₂*an-1 = (a₁*q)*(a₁*q⁽ⁿ⁻²⁾) = a₁²*q⁽ⁿ⁻¹⁾
Produto de terceiro termo com o antepenúltimo termo
a₃*an-2 = (a₁*q²)*(a₁*q⁽ⁿ⁻³⁾) = a₁²*q⁽ⁿ⁻¹⁾
...
Desta forma, fica fácil definir qual é o produto de todos os termos de uma PG. Veja só:
Produto = a₁*a₂*a₃*...*an. Como na multiplicação, a ordem dos fatores não altera o produto, podemos escrever esse produtório como:
Produto = (a₁*an)*(a₂*an-1)*(a₃*an-2)*... Como o valor dos produtos dentro dos parênteses é o mesmo (a₁²*q⁽ⁿ⁻¹⁾), como foi visto acima, e como esta sequência tem n termos, teremos (n/2) parênteses, já que cada parênteses tem dois termos. Assim:
Produto = [√(a₁²*q⁽ⁿ⁻¹⁾)]ⁿ = [a₁*√q⁽ⁿ⁻¹⁾]ⁿ.
Outro dado importante de se calcular, é a soma dos termos da PG. Existem várias formas de encontrar a fórmula da soma da PG (já foi feito neste blog por indução finita e soma telescópica), porém por ser de mais fácil compreensão, vou utilizar o método da soma telescópica (para quem não sabe o que é isso, vou explicar na medida que deduzo a fórmula)
O que queremos saber é a soma dos termos de uma PG, ou seja:
S = a₁ + a₂ + a₃ + ... + an
(1) S = a₁ + a₁*q + a₁*q² + ... + a₁*q⁽ⁿ⁻¹⁾. Se multiplicarmos esse somatório por q, teremos:
(2) q*S = a₁*q + a₁*q² + a₁*q³ + ... + a₁*qⁿ
Agora vamos subtrair as equações (2) de (1), fazendo (2) - (1), assim teremos:
q*S - S = (a₁*q + a₁*q² + a₁*q³ + ... + a₁*qⁿ) - (a₁ + a₁*q + a₁*q² + ... + a₁*q⁽ⁿ⁻¹⁾)
Perceba que podemos anular vários termos que são iguais (este método é chamado de soma telescópica, onde você cancela vários termos iguais pela subtração por serem termos iguais).
Desta forma, todos os termos serão cancelado com exceção de (a₁*qⁿ) e a₁.
Assim:
q*S - S = (a₁*qⁿ) - (a₁). Isolando os termos comuns dos dois lados:
S*(q-1) = a₁*(qⁿ - 1), logo:
S = [a₁*(qⁿ - 1)] / [q-1], onde S é a soma dos termos.
Para uma PG decrescente infinita a fórmula é a mesma só que, para que a PG seja decrescente, q deve ser menor que 1 e maior que zero. Assim, como ela tende a ter infinitos termos, ou seja, n tende ao infinito, qⁿ vai tender a zero (faça o teste, pegue um valor qualquer, entre zero e 1 e eleve a potências grandes. Perceberá que quanto maior é este potência, mais o resultado se aproxima de zero. No infinito, será zero).
Assim, na PG infinita:
S = [a₁*(qⁿ - 1)] / [q-1], como qⁿ = 0
S = [a₁*(- 1)] / [q-1].
S = [-a₁] / [q-1]. Multiplicando o numerador e o denominador por (-1), o que não muda em nada a fração, temos:
S = a₁ / [1-q]
Abaixo, alguns exercícios e explicações que foram usados os conceitos citados acima: